Geometría

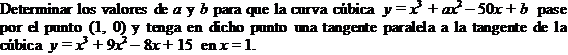
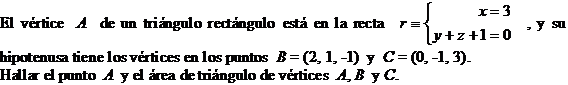
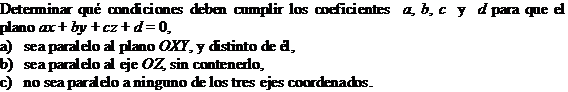
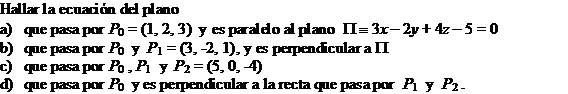
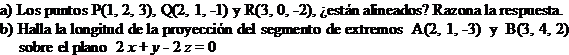
Dados los vectores hallar:

(a) El producto escalar de

(b) El ángulo que forman

(c) Un vector unitario, ortogonal a

(d) El área del paralelogramo determinado por los vectores

(e) El volumen del paralelepípedo determinado por los vectores

(f) El valor de x para que el vector (2,5,x) sea ortogonal a

Halla las ecuaciones paramétricas de la recta que pasa por el punto A(0,-1,3) y por el punto medio del segmento de extremos P(7,-1-4) y Q(1,5,2)

Halla la ecuación continua de la recta que pasa por el punto A(1,3,-1) y es perpendicular a los vectores

Halla:

(a) La ecuación de la recta s que pasa por P(0,0,1), perpendicular al plano

(b) La ecuación del plano P₁ que contiene a los puntos A(0,-1-2), B(1,0,2) y C(2,-1,0)

(c) La ecuación del plano P₂ que pasa por el punto Q(1,0,1) y es perpendicular a la recta

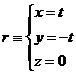
Sean los planos:

Se pide:

(a) Hallar m para que sean paralelos. Para este valor de m, calcular la distancia entre ambos planos

(b) Hallar m para que los planos sean perpendiculares.

Halla la ecuación del plano p perpendicular al plano h: 2x-y+3z-1 = 0, paralelo a la recta r: y que pasa por el origen. (1)

Dado el punto P(1,1,1) y la recta r: 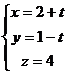calcula:

a) El plano p perpendicular a la recta r que pasa por el punto P. (0,5)

b) El punto de corte del plano p y la recta r. (1)

c) La distancia del punto P a la recta r. (0,5)

Dados los vectores u = (1,0,1) , v = (-2,1,1) y w = (0,-2,3):

a) Indica que forma tienen todos los vectores que son combinación lineal del vector u. Escribe tres ejemplos concretos.

b) Indica igualmente qué expresión tienen todos los vectores que son combinación lineal de los vectores v y w. Escribe tres ejemplos concretos.

c) Calcula x = v x w . Calcula el área del paralelogramo formado por los vectores v y w. ¿Cómo es el vector x con respecto a cualquier vector generado por v y w?

d) Calcula: u·x , |u| , |x| y el ángulo que forman los vectores u y x

e) Calcula el siguiente producto mixto: [u,w,v] . ¿Cuál es el volumen del paralelepípedo formado por los vectores u, v y w?

Dados el punto P(1,2,-3) y el vector u = (-4,1,-1), calcula:

a) El punto A resultante de aplicar el vector u al punto P.

b) El punto B tal que al aplicarle el vector u obtenemos el punto P.

c) El punto medio de A y B.

d) Las coordenadas de los vectores

e) El punto C que se encuentra en el segmento AB a doble de distancia de B que de A.

Dados el punto P(1,1,-2) y los vectores u = (2,1,0) y v = (0,3,-1). Calcula:

a) Las ecuaciones continua e implícitas de la recta r que pasa por el punto P con dirección u.

b) La ecuación general del plano p que pasa por el punto P con direcciones u y v.

c) Posición relativa de la recta r y el plano p. ¿Qué resulta de su intersección?

d) Calcula la ecuación continua de la recta perpendicular al plano p que pasa por el punto P.

e) Calcula la ecuación del plano p’ paralelo a p que pasa por el punto A(6,1,0)

Dadas las ecuaciones de la recta r: y del plano p: 3x-2y+z+2 = 0. Calcula:

a) Un punto y un vector director de la recta r; y un punto y el vector normal del plano p.

b) Posición relativa de la recta r y el plano p.

c) Indica la ecuación general de un plano que contenga a la recta r.

d) Calcula la ecuación continua de la recta paralela a r que pase por el origen.

e) Calcula la ecuación continua de una recta paralela al plano p que pase por el origen.